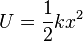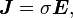The
Heisenberg uncertainty principle says that the more we know about where a
particle is right now, the less we know about how fast it's going and the direction that it's going. This also works the other way around (so the more we know about how fast it's going and the direction it's going, the less we know about where it is right now.)
An important part of quantum mechanics, which shows itself in the Heisenberg Uncertainty Principle, is that no physical event can be (really specifically) described as a "classic
point particle" or as a
wave, but rather the tiny event is best described in terms of
wave-particle duality. Basically, small bits of matter and small waves of energy are sometimes very hard to tell apart, because they can act like both at the same time.
The Heisenberg uncertainty principle is caused by this.
A quantum mechanical particle wave is sort of like a
sound wave. When people try to measure the
frequency of a sound wave, they are trying to figure out how often something happens in a given
amount of time. That means there's basically no such thing as "frequency" in one single moment of time. In order to be really have a sure frequency, a signal has to be around for a long time (which means it doesn't really exist in only a really specific "moment in time"). It works the other way, too: if a signal exists for only a second, it wasn't around long enough to have a really specific
frequency band. This is basically
Math's "version" of the Uncertainty Principle.
Physicists who studied light in the 1700's and 1800's were having a big argument about whether light was made of particles shooting around like tiny bullets, or waves washing around like water waves. At times, light seems to do both. At times, light seems to go only in a straight line, as if it were made of particles. But other experiments show that light has a frequency and wavelength, just like a sound wave or water wave. Until the 20th century, most physicists thought that light was either one or the other, and that the scientists on the other side of the argument were simply wrong.
In 1909, a scientist named Geoffrey Taylor decided that he was going to settle this argument once and for all. He borrowed an experiment invented earlier by Thomas Young, where light was shone through two small holes right next to each other. When bright light was shone through these two small holes, it created an interference pattern that seemed to show that light was actually a wave.
Taylor's idea was to photograph the film coming out of the holes with a special film that was unusually sensitive to light. When bright light was shined through the holes, the film showed an interference pattern, just like Young showed earlier. Taylor then turned down the light to a very dim level. When the light was dim enough, Taylor's photographs showed tiny pinpoints of light scattering out of the holes. This seemed to show that light was actually a particle. If Taylor allowed the dim light to shine through the holes for long enough, the dots eventually filled up the film to make an interference pattern again. This demonstrated that light was somehow both a wave and a particle.
To make matters even more confusing, Victor de Broglie suggested that matter might act the same way. Scientists then performed these same experiments with electrons, and found that electrons too are somehow both particles and waves.
Today, these experiments have been done in so many different ways by so many different people that scientists simply accept that both matter and light are somehow both waves and particles. Scientists generally admit that even they do not fully understand how this can be, but they are quite certain that it must be true. Although it seems impossible to understand how anything can be both a wave and a particle, scientists do have a number of equations for describing these things that have variables for both wavelength (a wave property) and momentum (a particle property). This seeming impossiblity is referred to as the wave-particle duality.
Particles as waves
An electron has a wavelength called the "de Broglie wavelength". It can be calculated using the equation
λD is the de Broglie wavelength.
h is
Planck's constant
ρ is the
momentum of the particle.
This made the idea that electrons in
atoms show a standing wave pattern
Waves as particles
The
photoelectric effect shows that a
light photon which has enough
energy (a high enough
frequency), can cause an electron to be released off a
metal's surface. Electrons in this case can be called
photoelectrons.
Quantum mechanics ("QM") is a part of
physics, which is the study of
matter and
energy. Quantum mechanics explains how things smaller than the size of
atoms act. The main things studied are called
subatomic particles and
electromagnetic waves.
Quantum is a
Latin word which means 'how much'. So a
quantum of energy is a definite amount of energy. Any lamp such as a
candle or
laser shoots out light
unit by unit. The more of these units (
photons) are given off per second, the brighter, or more intense, the light. The
wavelength (or
frequency) decides the color of the light.
Black at left is
ultraviolet; black at right is
infrared.
If the color of the light is
infrared (lower in
frequency than red light), each photon can heat up what it hits. So, if a strong infrared lamp (a
heat lamp) is pointed at a person, that person will feel warm, or even hot. However, the person cannot get a
sunburn, because the photons do not have enough energy to kill living cells. Infrared photons are sometimes called "black light" because humans cannot see infrared light. Humans can feel the radiation in the form of
heat. For example, a person walking by a brick building that has been heated by the sun will feel heat from the building without having to touch it.
If the color of the light is
ultraviolet (higher in frequency than violet light), then each photon has a lot of energy, enough to hurt skin cells and cause a sunburn. Even higher frequencies of light (or
electromagnetic radiation) cause even more damage.
X-rays can go deep into the human body and do things like kill cells. Humans cannot see or feel ultraviolet light. They may only know they have been under ultraviolet light when they get a sunburn. Areas where it is important to kill
germs often use
ultraviolet lamps to destroy
bacteria,
fungi, etc.
Quantum mechanics started when it was discovered that a certain frequency means a certain amount of energy. The higher the frequency, the more power a photon has, the more damage it can do. Quantum mechanics later grew to explain the internal
structure of atoms. Quantum mechanics also explains the way that a photon can
interfere with itself, and many other things never imagined in
classical physics.
Planck discovered the relationship between frequency and energy. Nobody earlier than he had guessed that frequency would be proportional to energy (this means that as one increases, the other does too). If we choose to use what are called
natural units, then the number representing the frequency of a photon would also represent its energy. The
equation would have been:
- e = f
But the way physics grew, there was no natural connection between the units then used to measure energy and the units commonly used to measure time (and therefore frequency). So the formula that Planck worked out to make the numbers all come out right was:
- e = h × f
-
-
r, energy equals
h times frequency. This
h is a special proportionality constant, called
Planck's constant, after its discoverer. Quantum mechanics is based on the realization that a photon of a certain frequency means a photon of a certain amount of energy. Besides that, a certain kind of atom can only give off certain frequencies of radiation, so it can also only give off photons that have certain amounts of energy.
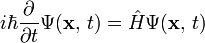
is the reduced Planck's constant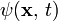
is the wavefunction
is the Hamiltonian energy operator
